My research is in the area of elliptic curve cryptography and related finite field arithmetic. I am interested in new cryptographic primitives, new algorithms in computational number theory, new protocols, efficient hardware and software implementations, and side-channel attacks and countermeasures.
Post-Quantum Cryptography
Presence of quantum computers is a real threat against the security of currently used public key cryptographic algorithms such as RSA and Elliptic curve cryptography. Post-quantum cryptography refers to research on cryptographic primitives (usually public-key cryptosystems) that are not efficiently breakable using quantum computers. This research investigates design, analysis, and implementation of quantum-safe cryptographic algorithms. For more information refer to PQCryptARM.
Finite Field Arithmetic
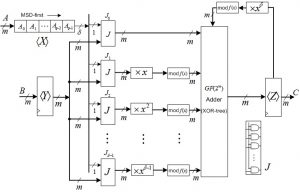
The arithmetic operations in the finite fields over prime fields and binary extension fields are largely utilized for cryptographic algorithms such as point multiplication in elliptic curve cryptography, exponentiation-based cryptosystems, and coding. This research investigates efficient algorithms and efficient architectures for the computation of finite field operations.
Efficient Implementations of Cryptographic Primitives
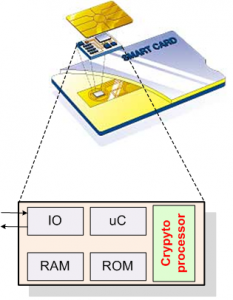
Providing security for the emerging deeply-embedded systems utilized in sensitive applications is a problem whose practical mechanisms have not received sufficient attention by the research community and industry alike. This research investigates efficient implementations of elliptic curve cryptography on embedded devices with extremely-constrained environments.
Machine-Level Optimization for the Computation of Cryptographic Pairings
High-speed computations of pairing-based cryptography is crucial for both desktop computers and embedded hand-held devices. This research investigates the machine-level and assembly optimizations for the computation of lower level finite field arithmetic used in pairings.
Highly-parallel scalable architectures for Cryptography Computations
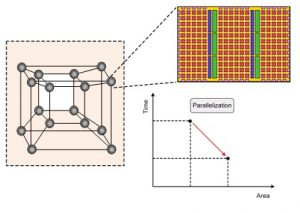
Highly-p
arallel and fast computations of the widely-used cryptographic algorithm is required for high-performance applications. However, a challenge to cope with is that most applications for which parallelism is essential, have significantly large scale that is not commonly supported by today’s algorithms. Therefore, new algorithms are required to investigate parallelization.
The prospect of quantum computers is a threat against the security of currently used public key cryptographic algorithms. It has been widely accepted that, both public key cryptosystems including RSA and ECC will be broken by quantum computers employing certain algorithms. Although large-scale quantum computers do not yet exist, but the goal is to develop quantum-resistant cryptosystems in anticipation of quantum computers as most of the public key cryptography that is used on the Internet today is based on algorithms that are vulnerable to quantum attacks.
This project will explore isogenies on elliptic curves as a foundation for quantum-resistant cryptography. Isogeny computation is known to be difficult. This project will analyze newer and faster families of isogenies, which yield a faster solution to the problem of finding isogenies. It will exploit state-of-the-art techniques and employ new optimizations to speed up the computation in isogeny-based cryptography, including tower field and curve arithmetic. The performance of field arithmetic computation is strongly influenced by the processor micro-architecture features, the size of the operands, the algorithms, and programming techniques associated to them. This research will provide preliminary results on developing fast algorithms and architectures for post-quantum cryptographic computations suitable for emerging embedded systems.
For more information click HERE.
Publications
- R. Azarderakhsh, D. Jao, K. Kalach, B. Koziel and Ch. Leonardi, “Key compression for isogeny-based cryptosystems”, in Proc. AsiaPKC 2016, pp. 1-10, ACM, Jun. 2016.
- B. Koziel, R. Azarderakhsh, A. Jalali, D. Jao, and M. Mozaffari Kermani, “NEON-SIDH: Efficient implementation of supersingular isogeny Diffie-Hellman key exchange protocol on ARM”, in Proc. Conf. Cryptology and Network Security, CANS 2016, to appear in 2016.
- B. Koziel, R. Azarderakhsh, D. Jao and M. Mozaffari Kermani, “On Fast Calculation of Addition Chains for Isogeny-Based Cryptography”, in Proc. Inscrypt 2016, pp.334-347, 2016.
- R. Azarderakhsh and K. Karabina, “Efficient Algorithms and Architectures for the Computation of Double Point Multiplication on Elliptic Curves”, in Proc. Third ACM workshop on Cryptography and Security in Computing Systems, CS2@HiPEAC 2016, ACM, pp.25-30, Jan. 2016.
There is a need for secure and practical alternatives to existing cryptosystems which are resistant to attacks by quantum computers and can be deployed today with as little disruption as possible. Also, there is a growing concern that over the next decade, advances in technology will not be able to deliver the level of performance and growth they have in the past. Highly-parallel and fast computations of the quantum-resistant cryptographic algorithms such as isogeny-based cryptosystems are required for high-performance applications. However, a challenge to tackle is that most applications that lend themselves to being parallelized, a key attribute for high-performance computing, have very significant scale that is rarely seen in the original algorithms proposed. Therefore, new algorithms and techniques are required to investigate parallelization and scalability in all levels of computations for isogeny-based cryptography over supersingular elliptic curves.Publications
- B. Koziel, R. Azarderakhsh, and M. Mozaffari Kermani, D. Jao, “Post-quantum cryptography on FPGA based on Isogenies on elliptic curves”, IEEE Transactions on Circuits and Systems (TCAS-I), vol. 64, no. 1, pp. 86-99, Jan. 2017.
- B. Koziel, R. Azarderakhsh, D. Jao and M. Mozaffari Kermani, “On Fast Calculation of Addition Chains for Isogeny-Based Cryptography”, in Proc. Inscrypt 2016, pp.334-347, 2016.
- B. Koziel, R. Azarderakhsh, D. Jao, “On Secure Implementations of Quantum-Resistant Supersingular Isogeny Diffie-Hellman”, poster, in Proc. HOST 2017, to appear 2017.